Reinventing the wheel
Posted by: stak
Posted on: 2007-05-05 14:04:37
People generally seem to think that reinventing the wheel is a bad thing. Although it can be bad sometimes, there are a lot of cases where it's much better to start from scratch and if necessary, reinvent the wheel. The problem with reusing the wheel is the same as with a lot of things: hidden assumptions. The person who invented the wheel designed it with a certain set of assumptions that weren't documented. Any time you attempt to reuse the wheel, it is quite possible that one or more of these assumptions won't hold, and so reusing the wheel is inefficient at best, and just plain wrong at worst.
One of the assumptions with the wheel, for instance, is that it will be used on a flat surface. If you use a wheel when going up an incline, it requires additional machinery (brakes) to prevent it from rolling back down. If you were to design a car that only went uphill, and you decided to reuse the wheel, you'd have to add a braking mechanism to go with it. On the other hand, if you decided to reinvent the wheel, you might end up with something that looked more like this:
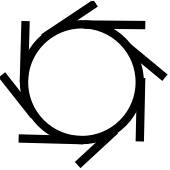
The things sticking out of the wheel would allow it to roll forward (towards the left in the picture above), and would prevent it from rolling backwards. No brakes required (assuming the wheel is strong enough to hold the weight of whatever it's carrying, etc.). Clearly, this solution is more efficient than having to add a complicated and unnecessary braking mechanism.
The same principle applies whenever the choice of reuse vs. reinvent comes up. More often than not, reinventing an item will be more efficient for the overall design, because the item will be redesigned while taking into account the specific context it will be used in. In software, this problem seems to come up over and over. The Ariane 5 disaster was a result of precisely this problem - code from the Ariane 4 was reused, and one of the assumptions (upper bound on acceleration) was no longer valid, resulting in a system failure.
If every system available for reuse were to document every single assumption about the context it expected to be used in, this probably wouldn't be too much of a problem. Although possible in theory, I'm pretty sure this is impossible in practice - most of the time people make assumptions without even being aware they're doing so. One solution is to simply never reuse anything, but that's just as stupid as blindly reusing everything. The correct solution lies somewhere in the middle - reuse whenever possible, but not before going over every explicit and as many implicit assumptions about the system as possible, and making sure that the costs are outweighed by the benefits.
|
Posted by Dave Pritchard at 2007-05-09 03:44:04
What's the difference between this design and a polygon? A polygon won't roll forward any more easily than it reads backwards, so I feel like I'm missing some key fact.
|
|
That's just it - a polygon won't roll forwards any more easily than it rolls backwards. The above design will roll forwards more easily than it rolls backwards, so it's better for uni-directional motion.
|
|
But, why does it roll forwards more easily? I can't think of any situation where the force/torque between the ground and the "wheel" would be any different than the corresponding force/torque between the ground and a polygon.
In other words, what makes the wheel different than its convex hull? Do you assume the ground is not a straight plane? |
|
The confusion seems to be because I think Kats is assuming it's a hard wheel (ala steel railroad wheels) and you're thinking it's a soft wheel (ala car tires). However, even if it's a soft wheel, it'll require more energy for the wheel to go back, because there is something (the little bits sticking out) increasing the force required to go backwards.
Something similar that may help visualize is a cog railway. |
|
I have assumed the thing is rigid (hard), and I'm not exactly sure what it would mean for this to be soft. Contrary to what you said, my initial claim is (and remains) that the "bits" have no effect on how hard it is to move, compared to a polygonal wheel.
To get a thing on "wheels" and an axle to move, you need to apply sufficient torque on the wheel to counteract the torque exerted by gravity, right? The necessary torque would be the same in either direction (in the rigid case). On the other hand, if you could selectively "fold" the pointy bits, that might reduce the amount of initial torque required to move... |
|
Maybe part of the problem was that I didn't make the pointy bits long enough in the picture. Consider a circle with radius r, and a pointy bit of length r sticking out at a tangent to the circle. The pointy bit will be perpendicular to the ground (and will touch the ground) at the exact point that the torque will be transferred down the pointy bit. The normal force from the ground on the pointy bit will counter the torque, cancelling it and stop the wheel from turning.
So the thing that I think you're missing is that last part - the angle at which the pointy bits intersect the ground changes the amount of normal force that will counter the torque applied, and will therefore change how hard it is to roll the wheel. |
|
I think my point remains valid (assuming it ever was, which I'm pretty sure of) regardless of the length of the spokes, or how many there are. As you point out, the force is transfered where the pointy bit touches the ground. I disagree with your "perpendicular" assertion.
>> the angle at which the pointy bits intersect >> the ground changes the amount of normal force [applied] This is also not true. Recall that a force vector F applied at a point P to a object whose axis lies at A is equal to the cross product ((P-A) x F). The direction of the pointy thing at point P is irrelevant. I tried to mimic your diagram (which has 8 spokes of length r, it appears). It's kind of shitty, sorry... the outer octagon is a convex hull, drawn only for emphasis. The left diagram shows the wheel at static equilibrium. There are 3 forces acting on the wheel, the normal force from the ground acting on the left pointy bit, the normal force from the ground acting on the right pointy bit, and gravity (which is applied on the centre of gravity = axis). These forces are labeled nl, nr, g. The net force is zero as is the net torque (as is required by a static equilibrium). In this case it's not hard to see that |AP| = sqrt(2)r. The torque from nr is |AP|*|g|/2*sin(phi) ccw, where |g| is the wheel's weight (i.e., mass times 9.8 m/s/s). Similarly nl exerts the same amount of torque but clockwise, and g exerts no torque. On the right you see another static equilibrium, upon applying a nearly-large-enough driving torque d to get the thing rolling to the right. You can calculate, based on the static equilibrium, that the torque d is equal to |AP|*|g|*sin(phi) cw. But the diagram to get it rolling left is symmetric and requires the same amount of torque, ccw. I tried to look for a pre-existing diagram and found this instead. After reading this it occurred to me that I should revoke my ``selectively "fold" the pointy bits'' comment since this would only convert gravitational potential energy to kinetic energy, and you'd have to expend the same energy to live your car back up the same amount... W00t high school physics! |
|
Nice free-body diagram.. :) Two points:
1. Your free-body diagram assumes the wheel is on a level surface. In my example, I said the wheel would only be used on an incline. If you do the free-body diagram of the wheel on an incline, you get a "horizontal" (assuming the slanted ground is the x axis) component to gravity, which must be countered by friction on the spokes. The friction will also contribute to torque, making nl and nr unequal in order to maintain equilibrium. This makes the applied torques (on the axle) required to get it rolling left and right unequal. In my rough free-body diagram for this, it turned out the torque required to get it rolling uphill is more than the torque required to get it rolling downhill, which makes sense. 2. This entire thing with the free-body diagram and torques required to make it roll left and right is kind of irrelevant to my original point. We got sidetracked somewhere along the way because of my poor choice of words. When I said "The things sticking out of the wheel would allow it to roll forward (towards the left in the picture above), and would prevent it from rolling backwards.", what I really meant was that "The things sticking out of the wheel allow it to be pulled forward (towards the left in the picture above), and will prevent it from rolling backwards in the absence of the pulling force." What this means is not that the wheel requires more torque to roll down than up. What it does mean is that the wheel can remain in static equilibrium on an incline when no torque is applied from the axle. This isn't possible in a regular wheel (sans spokes), since the friction force contributes torque, and causes the wheel to roll downhill in the absence of brakes/pulling force. This is possible with the reinvented wheel, since the normal force on one of the spokes provides a torque that will prevent the wheel from rolling downhill. |
|
Ah I completely missed the incline part... I now see what you meant.
It reminds me of programming contests... in terms of time spent due to not reading carefully =) |
|
the incline makes no difference. Allow the flaps to fold when going forward but not fold going backward. Like those spike strips on car exits.
|
|
but even if the were rigid, on any natural surface it would roll easier going forwards than backwards anyway because the spikes would "stick" in the ground going backwards, adding another dimension instead of just the polygonal length that is the same in each direction.
|
(c) Kartikaya Gupta, 2004-2025. User comments owned by their respective posters. All rights reserved.
You are accessing this website via IPv4. Consider upgrading to IPv6!